Most Common Hit Roulette Numbers
TheGambler’s fallacy is the mistaken perception that if an unbiased occasion hasnot occurred in a very long time, then it turns into overdue and extraseemingly. Additionally, it is equally incorrect that if a final result hasoccurred a disproportionate variety of occasions these days, in comparison withstatistical expectations, then it turns into overheated and fewer prone tohappen the subsequent time. An instance of this fallacious considering islikely to be that if the quantity 23 hasn’t been drawn in a 6-49 lottery thefinal 100 video games, then it turns into extra prone to be drawn through thesubsequent drawing. If you are wonder about what is the most hit number in roulette, you should continue to readthis article.
What happens if you do not want tocollect 100 hours of data on a single wheel?
Its the same with a roulette wheel, if you don't specify a particular number that must hit then there are lots of spins that can go by and there being some surviving number that is unhit is still quite likely. Ofcourse I don't want to know what number will NOT hit on that next spin, I want to know what number will hit on that next spin. Number 17 is really a special number and is located at the center of the roulette table. Number 17 is black. Number 23 and 24: These two numbers are also in the middle of the table, and many believe that the players are the most attentive. Many players believe that just these numbers are happy and put bets on them.
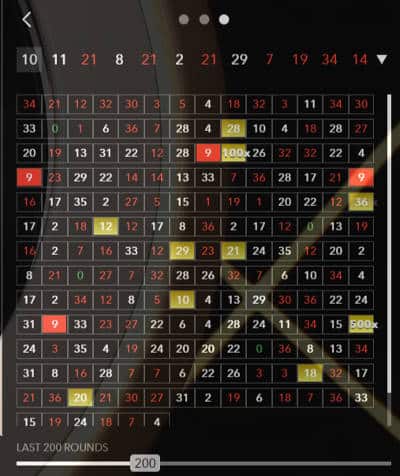
Some casinosare polite enough to give you the fourth “hottest” and “coolest”numbers of the last 300 rotations on a silver platter. The image at the top ofthe page shows an example taken on a double zero wheel in Venice.
If we consider the American roulette wheel, the most popular contiguous bet combination is based on the center column. The latter features the span (in a clockwise manner) from the numbers 23 to 5 with five gaps (0, 7, 9, 28, 30). In addition, two other numbers remain outside of the span (8 and 29). It is a very common tactic to bet on five roulette numbers per spin. There is also an automated Five Numbers Bet, that is called Neighbors bet. In the Neighbors bet, you bet a number and its four neighboring numbers: the two numbers on the left to the main number and the two numbers on the right, based on the European wheel layout.
For 300spins, the average number of wins per zero zero wheel for any number is 300/38= 7.9. Is this unusual? No. In the simulation simulation of more than 80billion, the most common number occurred in 300 tightening experiments, themost common occurrence was 27.4% 14 times. The most likely total of the second,third and fourth most common numbers were 13.9, 12, and 12, respectively, of37.9%, 46.5% and 45.8%, respectively. Therefore, the results of the “hottest” numbers in the pictureabove were a bit flatter than the average.
Thefollowing probability indicates the probability of double zero roulette in 300spins of the hottest four numbers. For example, the probability of the third most common number occurring 15times is 0.009210.
To place it in different phrases, it’s pure that some numbers will probably be “scorching” and a few “cool.” In reality, such variations from the implications are extremely predictable. Sadly, for roulette gamers, we do not know which numbers will probably be “scorching,” simply that a few of them virtually definitely will probably be. I might additionally like to emphasize, opposite to the Gambler’s Fallacy, that on a good roulette wheel that each quantity is equally probably each spin and it makes no distinction what has occurred previously. Lastly, it shouldn’t be interpreted that we give an endorsement to the 888 Online casinos, which we linked to earlier.
You can check our bitcoin casino list playing online casino games.
Related posts:
Relevant news
Bitcoin Millionaires List – 2020 Updated – INFOGRAPHIC
Hello, dear Icium.org readers. In this content, we will introduce you to people who have…
read more +Is it legal to play roulette online in the UK?
Being a real online casino traditional, roulette enjoys enormous recognition amongst online casino followers, particularly…
read more +What Is The Best Online Blackjack Site?
Finding the best blackjack site that offers trouble-free money withdrawals can be quite troublesome. With…
read more +Is online poker be rigged?
Online poker, on the entire, is just not rigged. The monetary incentives for the poker…
read more +What Is The Best Online Casino For UK Players?
British casino players have the highest standards of where they place their money. Therefore, the…
 read more +
read more +What Is The Best Online Poker Site For Beginners?
If you are beginner, you are the right places to get information about Best Online…
read more +For 300 spins the probability that a particular number will not show up is (37/38)^300 = 0.0335%. That's pretty small, but not zero. If you repeated this 300 spin experiment 3000 times, you'd only expect to completely miss your number on one of the trials.
I am trying to figure out how many spins would u say is it where a number statistically would have to come up
It is all about the degree of certainty.
For a 38 number wheel.
From http://wizardofvegas.com/member/nope27/blog/:
'The below table is for the probability of NOT hitting 'at least 1' number in x spins.
formula used from:http://wizardofodds.com/askthewizard/roulette.html
question #2 at WoO.
Wizards' Example: for 'at least 1' number NOT hitting in 200 spins
 Sum i=1 to 37 [(-1)^(i+1) × combin(38,i) × ((38-i)/38)^38] = 16.9845715651245%'
Sum i=1 to 37 [(-1)^(i+1) × combin(38,i) × ((38-i)/38)^38] = 16.9845715651245%'I have expanded the table below from the above blog.
I have also run 1 million spin simulations and have seen many numbers that did not appear in 500 spins.
I would say from the table 1000 spins would be a hard one to ever witness.
| spins | prob | 1 in | expected # of spins |
|---|---|---|---|
| 50 | 99.9999975% | . | . |
| 60 | 99.9991% | . | . |
| 70 | 99.967896% | . | . |
| 80 | 99.678210% | . | . |
| 90 | 98.452658% | . | . |
| 100 | 95.339700% | . | . |
| 110 | 89.728676% | . | . |
| 120 | 81.746470% | . | . |
| 130 | 72.133375% | . | . |
| 140 | 61.855739% | . | . |
| 150 | 51.774802% | 1.9 | 290 |
| 160 | 42.490296% | 2.4 | 377 |
| 170 | 34.326903% | 2.9 | 495 |
| 180 | 27.391862% | 3.7 | 657 |
| 190 | 21.649355% | 4.6 | 878 |
| 200 | 16.984572% | 5.9 | 1,178 |
| 210 | 13.249361% | 7.5 | 1,585 |
| 220 | 10.290675% | 9.7 | 2,138 |
| 230 | 7.966128% | 12.6 | 2,887 |
| 240 | 6.151027% | 16.3 | 3,902 |
| 250 | 4.740313% | 21.1 | 5,274 |
| 260 | 3.647758% | 27.4 | 7,128 |
| 270 | 2.803866% | 35.7 | 9,630 |
| 280 | 2.153364% | 46.4 | 13,003 |
| 290 | 1.652705% | 60.5 | 17,547 |
| 300 | 1.267822% | 78.9 | 23,663 |
| 310 | 0.972205% | 102.9 | 31,886 |
| 320 | 0.745304% | 134.2 | 42,935 |
| 330 | 0.571235% | 175.1 | 57,770 |
| 340 | 0.437748% | 228.4 | 77,670 |
| 350 | 0.335412% | 298.1 | 104,349 |
| 360 | 0.256975% | 389.1 | 140,091 |
| 370 | 0.196867% | 508.0 | 187,944 |
| 380 | 0.150810% | 663.1 | 251,973 |
| 390 | 0.115523% | 865.6 | 337,594 |
| 400 | 0.088490% | 1,130.1 | 452,028 |
| 500 | 0.006149% | 16,261.5 | 8,130,771 |
| 600 | 0.000427% | 234,067.2 | 140,440,306 |
| 700 | 0.000030% | 3,369,203.4 | 2,358,442,356 |
| 800 | 0.000002061985% | 48,496,952.1 | 38,797,561,717 |
| 900 | 0.000000143251% | 698,074,378.6 | 628,266,940,697 |
| 1000 | 0.000000009952% | 10,048,215,791.0 | 10,048,215,791,014 |
For a particular number not to come up in 300 spins I would agree with PapaChubby: (37/38)^300 = 0.0335%.
For at least one number not to come up, I think that guido111 has a good grip on the problem based on a solution given by the Wizard for the case of 200 spins, however the Wizard's logic may not be easy for everyone to follow. Here is another approach based on counting the ways the balls can be distributed to the numbers.
We assume that both the balls and the numbers are distinguishable. The numbers are distinguishable because they are all different and the balls are distinguished by the order in which they are thrown. There is a function T(m,n) that gives the number of ways that m distinguishable objects may be distributed to n containers such that every container has at least one object. The number of ways of distributing m objects to n containers without restriction is nm so the probability that all numbers will have been hit by at least one ball is T(m,n)/nm
Most Common Hit Roulette Numbers List
. Subtract this from 1 and that is the probability that at least one number will remain unhit. For m = 300 and n = 38 this evaluates to 0.01267822135, which agrees with guido111's result.It is always possible either for a particular number or for some number or other not to come up based on the inequality T(m,n) < nm.
The T function is discussed in several books on combinatorics. I shall be glad to provide a bibliography if anyone asks.
Its the same with a roulette wheel, if you don't specify a particular number that must hit then there are lots of spins that can go by and there being some surviving number that is unhit is still quite likely.
Ofcourse I don't want to know what number will NOT hit on that next spin, I want to know what number will hit on that next spin.
You are using a different (correct) formula to account for all possibilities.
I use to play a method (it did quite well for sometime), I tracked all numbers until only ONE left unhit. When I got to that point, I started a 110 progression on that one number. It was around a $3,600 BR. Like I said, I made ALOT of money BUT as usual, it slowly tanked. The 110 combined with how far back it last hit was well over 300 spins and on multiple occasions I might add so I stopped playing it. That particular method slowly lured me away from playing sleepers/due.
Ken
That's why several gambler's like you have become victims of the 'gambler's fallacy'.
.......and you Keyser are low on gas, better stop. Which city this week? I heard the 21/33 is hitting ALOT at a casino in Tucson. Pack up the car and away you go!! (LMAO) Talk about putting all your eggs in ONE basket.
Ken